Limit
Apa Itu Limit Fungsi Aljabar?
Pada dasarnya, limit adalah suatu nilai yang menggunakan pendekatan fungsi ketika hendak mendekati nilai tertentu. Singkatnya, limit ini dianggap sebagai nilai yang menuju suatu batas. Disebut sebagai “batas” karena memang ‘dekat’ tetapi tidak bisa dicapai. Lalu, mengapa limit tersebut harus didekati? Karena suatu fungsi biasanya tidak terdefinisikan pada titik-titik tertentu. Meskipun suatu fungsi itu seringkali tidak terdefinisikan oleh titik-titik tertentu, tetapi masih dapat dicari tahu berapa nilai yang dapat didekati oleh fungsi tersebut, terlebih ketika titik tertentu semakin didekati oleh “limit”.
Definisi akan limit fungsi ini ternyata juga dapat dijelaskan secara aljabar lho… Misalkan f adalah fungsi yang terdefinisi pada interval tertentu yang memuat a, kecuali di a itu sendiri, sedangkan L adalah suatu bilangan riil. Maka fungsi f dapat dikatakan memiliki limit L untuk x mendekati a, sehingga ditulis Namun, hanya jika untuk setiap bilangan kecil ε > 0 terdapat bilangan δ > 0 sedemikian rupa sehingga jika 0 < |x-a| <δ maka |f(x)-L| <ε. Pernyataan tersebut dinamakan definisi limit secara umum.
Rumus Limit
Dalam ilmu matematika, konsep limit ini ditulis berupa:
Maksudnya, apabila x mendekati a tetapi x tidak sama dengan a, maka f(x) akan mendekati L. Pendekatan x ke a ini dapat dilihat dari dua sisi, yakni sisi kiri dan sisi kanan. Nah, dengan kata lain bahwa x juga dapat mendekati dari arah kiri dan arah kanan sehingga nantinya akan menghasilkan limit kiri dan limit kanan.
Maka dari itu, diperolehlah pernyataan bahwa:
0 <|x-p|<δ⇔|f(x) – L|ε
Maksudnya, suatu fungsi dapat dikatakan memiliki limit apabila antara limit kiri dan limit kanan juga mempunyai besar nilai yang sama. Apabila limit kiri dan limit kanan tidak sama, maka nilai limitnya juga tidak akan ada.
Sifat Fungsi Limit Aljabar
Apabila n adalah bilangan bulat positif, k adalah konstanta, f dan g adalah fungsi yang mempunyai limit di c, maka sifat-sifatnya akan berupa:
Metode Dalam Pemecahan Limit Fungsi Aljabar
Ada beberapa metode yang lebih sederhana untuk menentukan limit, yakni dengan metode substitusi, memfaktorkan, dan merasionalkan penyebut. Bagaimana saja cara yang diterapkan dalam metode-metode tersebut, yuk simak ulasan berikut!
1. Menentukan Limit dengan Substitusi
Apabila nilai suatu fungsi untuk x mendekati a, yang mana a adalah bilangan riil, maka dapat ditentukan dengan cara substitusi. Dalam cara substitusi ini nantinya akan mengganti nilai x dengan a. Namun, apabila hasilnya menjadi (∞-∞) atau 0/0 ∞/∞. Maka cara ini tidak dapat diterapkan secara langsung. Ada baiknya jika fungsi yang diambil limitnya itu perlu disederhanakan lagi. Perhatikan contoh berikut.
hasil dari limit adalah Dengan demikian, hasil dari limit adalah 1.
B. Teorema limit
Teorema Limit
Limit dalam bahasa umum bermakna batas.
Definisi dari limit ini menyatakan bahwa suatu fungsi f(x) akan mendekati nilai tertentu jika x mendekati nilai tertentu.
Pendekatan ini terbatas antara dua bilangan positif yang sangat kecil yang disebut sebagai epsilon dan delta.
Hubungan ke-2 bilangan positif kecil ini terangkum dalam definisi limit.
Limit 0/0
Bentuk 0/0 kemungkinan timbul dalam
ketika kita menemukan bentuk seperti itu coba untuk sederhanakan fungsi tersebut.
Jika itu bentuk persamaan kuadrat kita bisa coba memfaktorkan atau dengan cara asosiasi, dan jangan lupa aturan a2-b2 = (a+b) (a-b).
Berikut adalah contohnya :
Limit ∞/∞
Bentuk limit ∞/∞ terjadi pada fungsi suku banyak (polinom) seperti :
Rumus cepat limit bentuk ∞/∞
- Jika m<n maka L = 0
- Jika m=n maka L = a/p
- Jika m>n maka L = ∞
Limit (∞-∞)
Bentuk (∞-∞) sering sekali muncul pada saat ujian nasional.
Bentuk soalnya sangat beragam. Namun, penyelesaiannya tidak jauh dari penyederhanaan.
Jika disubstitusikan x -> 1 maka bentuknya akan mmenjadi (∞-∞).
Dan untuk menghilangkan bentuk ∞-∞ kita sederhanakan bentuk tersebut menjadi
Rumus Cepat limit tak hingga
Rumus cepat mengerjakan limit tak hingga yang pertama dapat digunakan untuk bentuk soal limit tak hingga pada bentuk pecahan.
Untuk memperoleh nilai limit tak hingga bentuk pecahan kita hanya perlu memperhatikan pangkat tertinggi dari masing-masing pembilang dan penyebut.
Ada 3 kemungkinan yang dapat saja terjadi.
- Pertama, pangkat tertinggi pembilang lebih kecil dari pangkat tertinggi penyebut.
- Kedua, pangkat tertinggi pembilang sama dengan pangkat tertinggi penyebut.
- Ketiga, pangkat tertinggi pembilang lebih tinggi dari pangkat tertinggi penyebut.
Rumus ke-3 nilai limit tak terhingga bentuk pecahan tersebut dapat dilihat pada persamaan dibawah ini.
Nilai pangkat tertinggi pada pembilang adalah 3. Nilai pangkat tertinggi penyebut adalah 2 (m>n). Jadi, nilai limitnya adalah ∞.
C. Limit tak tentu
Dalam kalkulus dan cabang lain analisis matematika, batasan yang melibatkan kombinasi aljabar fungsi dalam variabel independen sering kali dapat dievaluasi dengan mengganti fungsi; jika ekspresi yang diperoleh setelah substitusi ini tidak memberikan informasi yang cukup untuk menentukan batas aslinya, maka dikatakan menganggap file Bentuk tak tentu. Lebih khusus lagi, bentuk tak tentu adalah ekspresi matematika yang melibatkan nilai , dan , diperoleh dengan menerapkan teorema limit aljabar dalam proses mencoba menentukan nilai limit, which gagal untuk membatasi nilai limit tersebut pada satu nilai tertentu dan dengan demikian belum menentukan nilai limit tersebut.[1][2] Istilah ini awalnya diperkenalkan oleh murid Cauchy Moigno di pertengahan abad ke-19.
Ada tujuh bentuk tak tentu yang biasanya dipertimbangkan dalam literatur:[2]
Contoh paling umum dari bentuk tak tentu terjadi saat menentukan batas rasio dua fungsi, di mana kedua fungsi ini cenderung nol dalam batas, dan disebut sebagai "bentuk tak tentu dari ". Contohnya, sebagai pendekatan nilai , rasio dari , , dan saat menentukan , , dan dari nilai masing-masing. Dalam setiap kasus, jika batas pembilang dan penyebut diganti, ekspresi yang dihasilkan adalah nilai , yang tidak ditentukan. Dengan cara berbicara yang santai, dapat menerima nilai-nilainya , , atau , dan mudah untuk membuat contoh serupa yang batasannya adalah nilai tertentu.
Jadi, mengingat bahwa dua fungsi dan keduanya mendekat sebagai mendekati beberapa nilai limit , fakta itu saja tidak memberikan informasi yang cukup untuk mengevaluasi limit
Tidak setiap ekspresi aljabar yang tidak terdefinisi sesuai dengan bentuk tak tentu. Contohnya ekspresi tidak ditentukan sebagai bilangan real tetapi tidak sesuai dengan bentuk tak tentu, karena batas apa pun yang memunculkan bentuk ini akan menyimpang hingga tak terhingga.[3]
Ekspresi yang muncul dengan cara lain selain dengan menerapkan teorema aljabar batas dapat mengambil bentuk yang sama sebagai salah satu bentuk tak tentu. Namun, tidaklah tepat menyebut ungkapan ini sebagai "bentuk tak tentu" di luar konteks penentuan batas. Kasus yang paling umum adalah , yang mungkin, misalnya, muncul dari penggantian dari dalam persamaan . Ekspresi ini tidak terdefinisi, seperti pembagian dengan nol pada umumnya. Kasus lainnya adalah ekspresi . Apakah ekspresi ini dibiarkan tidak terdefinisi, atau ditentukan sama , tergantung pada bidang aplikasi dan mungkin berbeda antar penulis. Untuk lebih lanjut, lihat artikel Nol pangkat nol. Catat itu dan ekspresi lain yang melibatkan tak terhingga bukan bentuk tak tentu.



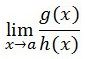





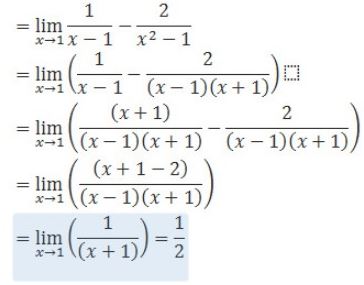
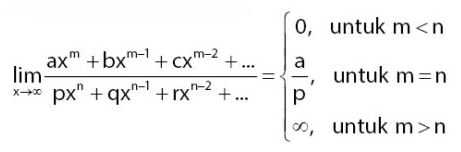



















Comments
Post a Comment