Integral Fungsi Aljabar
Nama: Muhammad Reviyata Satria Putra Prawira
Kelas: XI IPS 3
Absen: 17
A. Integral tak tentu
Apa Itu Integral Tak Tentu?
Integral merupakan anti turunan atau kebalikan dari turunan yang berfungsi untuk menentukan daerah, volume, titik pusat, dan lainnya.
Kalau suatu fungsi f(x) dibalik menjadi f’(x) maka itu merupakan turunan. Nah, jika f’(x) dibalik lagi menjadi f(x), maka itu merupakan integral.
Sebelum ke rumus integral tak tentu, elo perlu paham konsep turunan nih. Gue kasih bayangin dikit tentang turunan secara umum.
y= X3 Turunan dari soal ini berapa?
dydx = 3×2 Setelah diturunkan seperti ini, lalu dikali silang.
dy = 3×2 dx
d(X3) = 3×2 dx Bisa dilihat ya, y diganti dengan X3
Nah, dari sini bisa kita simpulkan ya cara mencari turunan bentuknya akan seperti ini nih.
Turunan dari X2 akan menjadi d(X2) = 2x dx
Turunan:
Sekarang kita balik, dikalikan silang ya:
df(x) = f’(x)dx
Kita tambahkan aja lambang integral (∫), menjadi:
∫df(x) = ∫f’(x)dx
∫f’(x)dx = f(x)+C
Pengertian integral tak tentu (indefinite integral) merupakan suatu fungsi baru yang punya turunan dari fungsi aslinya dan fungsi tersebut belum memiliki nilai pasti. Itulah mengapa dalam integral tak tentu ada konstanta (C).
Rumus Integral Tak Tentu
Oke, kita tahu kalau integral tak tentu berarti nilai atau batasannya belum pasti, sehingga ada nilai konstanta di dalamnya. Sekarang, mari kita definisikan seperti apa sih rumus dasar integral tak tentu? Perhatikan rumus di bawah ini.
Rumus Integral tak tentu:
Supaya lebih mudah dipahami, gue langsung cemplung angka-angkanya ke rumus di atas ya.
Nah, jelas ya sekarang? Jadi, elo hanya perlu memasukkan angka-angkanya ke dalam template rumus di atas. Sampai sini udah mulai paham dikit-dikit lah ya, tapi sebelum buru-buru ke contoh soal integral tak tentu, simak dulu sifat-sifatnya.
Sifat-Sifat Integral Tak Tentu
Pengertian udah tahu, rumus juga elo udah tahu, kurang lengkap rasanya kalau kita gak mengenal sifat-sifat dari integral tak tentu. Berikut adalah sifat-sifat integral tak tentu:

Ketika kamu memahami ketiga sifat di atas, saya yakin kamu akan lebih mudah dalam menghadapi integral ke depannya.
Contoh Soal Integral
Dalam soal ini, batas atas adalah 1 dan batas bawah -2. Tahap pertama yang perlu kita lakukan adalah melakukan integral fungsi 3x2+ 5x + 2 menjadi seperti di bawah ini.
Setelah kita mendapatkan bentuk integral dari fungsi tersebut, kita dapat memasukkan nilai batas atas dan bawah ke dalam fungsi tersebut lalu mengurangkannya menjadi seperti berikut.
Hasil dari integral tersebut adalah 27,5.
Untuk mengerjakan soal ini, kita dapat mencontoh cara pada soal sebelumnya yaitu melakukan integral fungsi terlebih dahulu kemudian mencari nilai p berdasarkan hasil 78 seperti berikut ini.
Setelah kita mendapatkan fungsi integral, kita dapat memasukkan batas atas dan bawah ke dalam fungsi tersebut.
Setelah memasuki fungsi pertidaksamaan tersebut, kita dapat menggunakan sifat pertidaksamaan untuk menyelesaikan soal tersebut sehingga didapatkan nilai P adalah 4. Maka untuk nilai -2p, kita dapat memasukkan nilai 4, maka hasil -2p= -8.
3. Tentukanlah integral x jika f’(x) = 3x2
Dalam mengerjakan soal ini, kita harus memperhatikan fungsi secara seksama. Dalam soal tersebut fungsi berbentuk f’(x) yang menandakan bahwa fungsi tersebut merupakan suatu turunan dari fungsi tertentu. Untuk mengerjakan soal tersebut, kita dapat menggunakan sifat dasar integral tak tentu seperti di bawah.seperti di bawah.
Sehingga nilai integral dari fungsi tersebut adalah x3+C
4. Tentukanlah integral x jika diketahui g’(x) = 3x5+3
Untuk mengerjakan soal ini, kita dapat menggunakan sifat seperti soal pertama. Dalam soal ini, g’(x) merupakan turunan dari suatu fungsi. Berikut ini cara penyelesaiannya
Nilai integral dari g’(x) adalah g(x) = (1/2)x6 + 3x + C
Di atas adalah contoh soal & pembahasan integral sederhana. Untuk kumpulan soal integral lainnya, lanjut di contoh soal berikutnya ya!
B. Teknik Pengintegralan
Teknik Pengintegralan: Metode Substitusi
Dalam memecahkan/menyelesaikan masalah integral tak tentu terutama untuk beberapa fungsi yang belum tercantum pada laman Primitif Fungsi, diperlukan teknik-teknik tertentu yang selanjutnya disebut teknik pengintegralan. Pada kesempatan kali ini akan dibahas mengenai salah satu teknik pengintegralan yang dikenal dengan sebutan metode substitusi.
Dalam menyelesaikan masalah integral tak tentu, masalah yang ada harus dibawa ke salah satu atau beberapa bentuk integrand yang telah dikenal. Dengan memasukkan atau mensubstitusi variabel baru yang tepat sehingga bentuk yang tadinya belum dikenal primitifnya berubah menjadi bentuk yang telah dikenal.
Diberikan fungsi |
Untuk membuktikan hal tersebut, maka cukup ditunjukkan bahwa derivatif kedua ruang terhadap merupakan fungsi yang sama. Diperhatikan bahwa
Sementara di lain pihak, diperoleh:
Dengan demikian, terbukti bahwa
Contoh.
- Akan ditentukan nilai integral tertentu dari
, untuk suatu konstanta
.
Penyelesaian:
Diambil substitusiatau
maka
. Dengan demikian,
Diperhatikan bahwa nilai
merupakan bentuk intergal yang telah dikenal.
- Akan ditentukan nilai integral tertentu dari
.
Penyelesaian:
Dengan substitusimaka diperoleh
, sehingga diperoleh integrasi:
Diperhatikan bahwa nilai
merupakan bentuk integral yang telah dikenal.
- Tentukan
.
Penyelesaian:
Disubstitusikan, sehingga diperoleh
. Akibatnya,
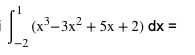
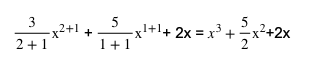
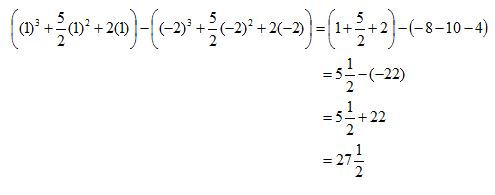
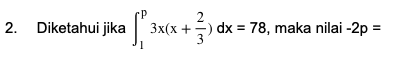
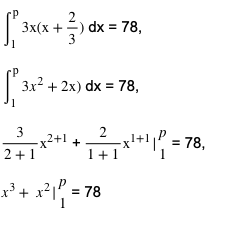
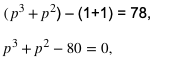
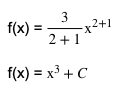
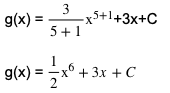

Comments
Post a Comment