Barisan & Deret

 Nama: Muhammad Reviyata Satria Putra Prawira

Kelas: XI IPS 3

Absen: 17

A. Barisan dan deret aritmatika

Baris dan Deret Aritmatika

Sebetulnya barisan dan deret terbagi menjadi beberapa macam. Tapi, kali ini gue hanya akan membahas mengenai baris dan deret aritmatika.

Di atas tadi sempat gue singgung sedikit mengenai apa itu barisan. Barisan adalah daftar bilangan yang dituliskan secara berurutan dari kiri ke kanan, di mana ia mempunyai pola atau karakteristik bilangan tertentu. Barisan biasanya disimbolkan dengan Un;

Sedangkan deret adalah penjumlahan dari suku-suku yang ada di dalam suatu barisan tertentu. Deret ini biasanya disimbolkan dengan Sn;

Kemudian aritmetika adalah ilmu berhitung dasar yang mencakup penjumlahan, pengurangan, perkalian, dan pembagian, yang ada di dalam cabang ilmu pengetahuan matematika. Psstt, inget lho, ejaan yang benar itu ‘aritmetika’, bukan ‘aritmatika’.

Rumus Baris dan Deret Aritmetika

Bentuk Umum Barisan Aritmetika

 dengan  bilangan asli

Rumus Suku ke-n

atau

Keterangan:

 = suku ke-n

 = a = suku pertama
n = jumlah atau banyaknya suku
b = beda atau selisih

Rumus Beda atau Selisih

Keterangan:

b = beda atau selisih

 = suku ke-n
 = suku sebelum suku ke-n

Rumus Suku Tengah

atau

Jika jumlah atau banyak suku dari suatu barisan aritmetika adalah ganjil, maka rumus untuk mencari suku tengahnya adalah sebagai berikut:

Keterangan:
 = suku tengah
 = suku terakhir
a = suku pertama
n = jumlah atau banyaknya suku

Kalau jumlah atau banyak sukunya genap, gimana tuh? Itu berarti barisan aritmetika tersebut nggak ada suku tengahnya, Sob.

Rumus Sisipan

Nah, gimana jadinya kalau elo menyisipkan bilangan dengan jumlah k ke dalam barisan aritmetika yang udah ada? Pastinya hal tersebut akan menyebabkan terbentuknya barisan aritmetika yang baru dan beberapa rumus di bawah ini juga ikut berubah, nih.

atau

Keterangan:

 = jumlah atau banyaknya suku barisan aritmetika baru
n = jumlah atau banyaknya suku barisan aritmetika lama
k = jumlah atau banyaknya bilangan yang disisipkan ke barisan aritmetika lama
 = beda atau selisih barisan aritmetika baru
b = beda atau selisih barisan aritmetika lama

Rumus-Rumus Deret Aritmetika

Bentuk Umum Deret Aritmetika

 dengan  bilangan asli

Rumus Suku ke-n

atau

Keterangan:
 = suku ke-n
 = suku ke-n
 = a = suku pertama
n = jumlah atau banyaknya suku
b = beda atau selisih

Contoh Soal Barisan dan Deret Aritmatika

Biar elo semua makin pol ngerti, coba cermati beberapa contoh soal cerita barisan aritmatika dalam kehidupan sehari hari dan deret aritmetika di bawah ini, ya!

Contoh Soal 1

Terdapat sebuah barisan bilangan seperti berikut 3, 5, 7, 9, …
Berapakah suku ke-30 dari barisan tersebut?

Pembahasan
Diketahui:
a = 3
b = 
= 5-3
= 2
Ditanyakan: U30?
Jawab:

= 3 + (30-1)2
= 3 + (29)2
= 3 + 58
= 61

Jadi, suku ke-30 dari barisan aritmetika tersebut adalah 61.

Contoh Soal 2

Terdapat sebuah barisan aritmetika sebagai berikut: 2, 6, 10, 14, …, 74. Berapa nilai suku tengahnya? Terletak pada suku ke berapa nilai tengah tersebut?

Pembahasan
Diketahui:
1. a = 2
2. b = 
= 6-2
= 4
3.  = 74

Ditanyakan:

a). ?

b). t suku tengah?

Jawab:
a). ?

= 1/2(2+74)
= 1/2(76)
= 38

Jadi, nilai suku tengah dari barisan aritmetika tersebut adalah adalah 38.

b). t suku tengah?

74 = 2 + (n-1)4
74 = 2 + 4n-4
74 = 4n – 2
74 +2 = 4n
76 = 4n
76/4 = n
19 = n

Jadi, jumlah atau banyaknya suku ada 18.

t = 1/2(n +1)
t = 1/2(19 +1)
t = 1/2(20)
t = 10.

Maka, suku tengah pada barisan aritmetika tersebut terletak pada suku ke-10.

Contoh Soal 3

Terdapat sebuah barisan aritmetika sebagai berikut 20 + 18 + 16, …
Tentukan berapa jumlah 12 suku pertamanya!

Diketahui:
a = 20
b = 2
Ditanyakan: Sn?
Jawab:

 =  (20 + 20 + (12-1)2))
= 6 (40 + 24 – 2)
= 6 (62)
= 372.

Jadi, jumlah 12 suku pertama dari barisan aritmetika tersebut adalah 372.

B. Barisan dan Deret Geometri

Pengertian Barisan dan Deret Geometri

Ilustrasi sempoa (Dok. Pixabay)

Barisan dan deret geometri adalah salah satu materi yang dipelajari dalam Matematika SMA. Barisan geometri adalah baris yang nilai setiap sukunya didapatkan dari suku sebelumnya melalui perkaliandengan suatu bilangan. 

Perbandingan atau rasio antara nilai suku-suku yang berdekatan selalu sama yaitu r. Nilai suku pertama dilambangkan dengan a.

Untuk mengetahui nilai suku ke-n dari suatu barisan geometri dapat dihitung dengan rumus berikut.

Sedangkan, deret geometri adalah penjumlahan suku-suku dari barisan geometri.

Penjumlahan dari suku-suku pertama sampai suku ke-n barisan geometri dapat dihitung dengan rumus berikut.

dengan syarat r < 1

atau

dengan syarat r > 1

Contoh Soal Barisan dan Deret Geometri

Contoh Soal 1: Soal Khusus

Selembar kertas dipotong menjadi dua bagian. Setiap bagian dipotong menjadi dua dan seterusnya. Jumlah potongan kertas setelah potongan kelima sama dengan… 

Pembahasan:

Diketahui: a = 1

r = 2

Ditanya: 

Jawab: 

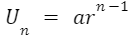
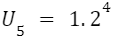
= 16

Jadi, jumlah potongan kertas setelah potongan kelima adalah 16

Contoh Soal 2

Pada sebuah deret geometri diketahui bahwa suku pertamanya adalah 3 dan suku ke-9 adalah 768. Suku ke-7 deret tersebut adalah…

Pembahasan:

Diketahui: a = 3

Ditanya: 

Jawab:

Sebelum kita mencari nilai dari  , kita akan mencari nilai r terlebih dahulu.

Ingat kembali bahwa  sehingga   dapat ditulis menjadi

Sehingga,

Jadi, suku ke-7 deret tersebut adalah 192.

Contoh Soal 3

Diketahui suku ke-5 dari barisan geometri adalah 243, hasil bagi suku ke-9 dengan suku ke-6 adalah 27. Suku ke-2 dari barisan tersebut adalah…

Pembahasan

Dalam contoh soal barisan dan deret geometri di atas, diketahui 

Ditanya  
Jawab:

Sebelum kita mencari nilai dari , kita akan mencari nilai a dan r terlebih dahulu.

Ingat kembali  maka

Substitusikan r = 3 ke persamaan  

sehingga

= 9

Jadi, suku ke-2 dari barisan tersebut adalah 9.

Contoh Soal 4

Jumlah 6 suku pertama deret geometri 2 + 6 + 18 + … adalah…

Pembahasan

Diketahui: a =  2

r = 3

ditanyakan 

Jawab:

Jadi, jumlah 6 suku pertama deret geometri tersebut adalah 728.

C. Bunga penyusutan pertumbuhan dan peluruhan.

1. Pertumbuhan

Pertumbuhan merupakan kenaikan atau pertambahan nilai suatu besaran terhadap besaran sebelumnya.Peristiwa yang termasuk dalam pertumbuhan adalah pertambahan penduduk dan perhitungan bunga majemuk di bank. Terdapat dua jenis pertumbuhan, yaitupertumbuhan eksponensial dan pertumbuhan linier.

Contoh:

Banyak penduduk kota A setiap tahun meningkat 2% secara eksponensial dari tahun sebelumnya. Tahun 2013 penduduk di kota A sebanyak 150.000 orang. Hitung banyak penduduk pada tahun 2014 dan 2023!

Jawab:

Banyak penduduk pada tahun 2014 (artinya 1 tahun setelah 2013, maka n = 1):

Banyak penduduk pada tahun 2023 (n=2023-2013=10):

2. Peluruhan

Peluruhan merupakan penurunan atau pengurangan nilai suatu besaran terhadap nilai besaran sebelumnya. Peristiwa yang termasuk dalam peluruhan (penyusutan) di antaranya adalah peluruhan zat radioaktif dan penurunan harga barang.

Contoh:

Suatu bahan radioaktif yang semula berukuran 125 gram mengalami reaksi kimia sehingga menyusut 12% dari ukuran sebelumnya setiap 12 jam secara eksponensial. Tentukan ukuran bahan radioaktif tersebut setelah 3 hari!

Jawab:

Peluruhan terjadi setiap 12 jam, sehari peluruhan terjadi 2 kali, 3 hari = 72 jam terjadi 6 kali peluruhan.

Referensi:

A:https://www.zenius.net/blog/barisan-dan-deret-aritmetika

B:https://www.zenius.net/blog/contoh-soal-barisan-dan-deret-geometri

C:https://www.ruangguru.com/blog/pertumbuhan-dan-peluruhan-matematika